数学系李海中完成的“Pinkall-Sterling猜想和超曲面几何的研究”项目获2019年度国家自然科学奖二等奖。

1989年U.Pinkall和I.Sterling在顶尖数学期刊Ann.Math. 论文提出Pinkall-Sterling 猜想: 三维球面中常平均曲率的嵌入环面是旋转环面。该项目给出三维球面中常平均曲率嵌入环面的完全分类，完全解决了 Pinkall-Sterling 猜想，结果可以叙述如下。

定理：3维球面中常平均曲率H的嵌入环面M必为旋转环面。当H＝0或H²＝1/3时，M必为Clifford 环面 S¹×S¹。对于任意的m≥2，

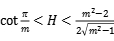，则存在唯一的常平均曲率H的嵌入环面（非Clifford环面）。

对于给定的H (H≠0, H²≠1/3)，得到平均曲率为H的新曲面可能不只一个，H越大，新曲面的个数越多。例如，当H=0.35时，只有1个新的CMC 环面，对应m=2；当H=3时，得到共有3 个不同的CMC 环面，对应的m 依次为7,8,9。

m=2, H=0.35 m=7, H=3

m=8, H=3. m=9, H=3